Have you ever wondered why some studies produce groundbreaking results while others fall flat? Often, the secret ingredient isn’t luck—it’s statistical power.
Imagine spending months on an experiment only to find that your results are inconclusive. It’s a frustrating scenario, but it happens all the time. The culprit is often a lack of power, which undermines your ability to detect real experimental effects. Without it, even the most brilliant research can be dismissed as invalid.
At its core, understanding power is about ensuring your study is strong enough to deliver trustworthy conclusions.
So, What Exactly is Power?
In simple terms, statistical power is the probability of detecting an effect when there actually is one.
Think of it like a smoke detector. A good detector (high power) will sound the alarm when there’s a fire. A faulty one (low power) might stay silent, leaving you unaware of the danger. In research, a low-powered study might fail to detect a real effect, leading you to believe there’s no fire when there actually is.
Power is expressed as a probability, ranging from 0% to 100%. The higher the power, the more likely you are to find a true effect.

A Real-World Example: Testing a New Drug
Let’s say a new drug is developed that improves cancer outcomes by 10% on average. We test it on 200 patients. Based on this, we’d expect:
- 20 patients to show improvement (the drug has a real effect).
- 180 patients to show no improvement.
Now, let’s introduce a statistical test to analyze the results. No test is perfect, so we’ll assume our test has a 5% error rate, meaning it might occasionally say the drug works when it doesn’t (a “false positive”).
Here’s where power comes in.
The Impact of Low Power (20%)
If our study has only 20% power, it means our test can only detect the drug’s true effect in 20% of the patients who actually benefit.
- Out of the 20 patients who should improve, our test will only identify 4 of them.
- The other 16 are missed opportunities—real effects that our study failed to see.
Meanwhile, the test’s 5% error rate on the 180 non-responding patients creates 9 false positives (5% of 180).
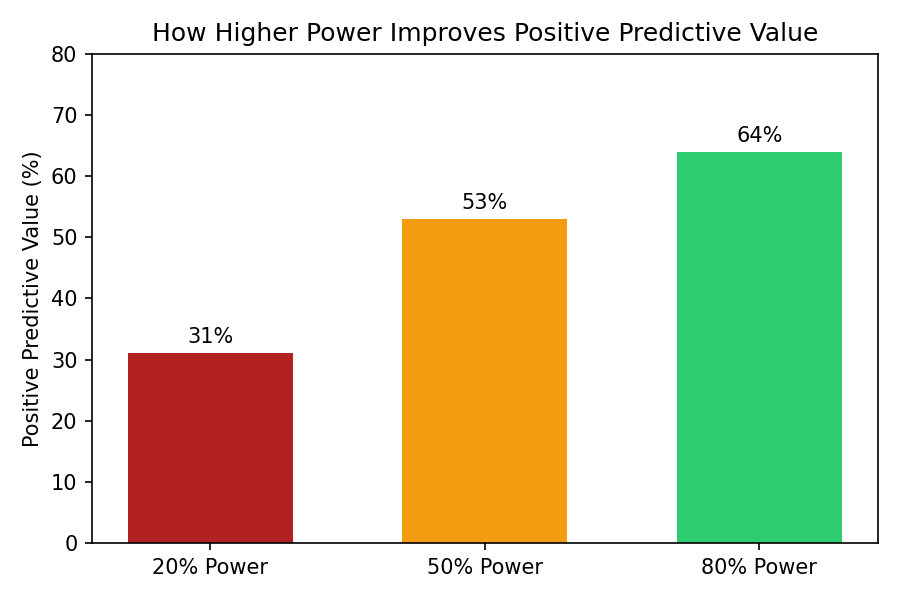
So, our test flags a total of 13 patients (4 true effects + 9 false positives). This means that when our test gives a positive result, it’s only correct 4 out of 13 times—just 31% of the time! That’s worse than a coin flip. A study this weak is practically useless.

The Difference Higher Power Makes (50% and 80%)
What happens if we increase the power?
- With 50% power, our test identifies 10 of the 20 true effects. Now, our positive results are correct 10 out of 19 times (53%). Better, but still not great.
- With 80% power, the gold standard in many fields, our test identifies 16 of the 20 true effects. The positive results are now correct 16 out of 25 times (64%). This is a much more reliable and trustworthy outcome.
Here’s a simple breakdown:
| Power Level | Positive Predictive Value (PPV) |
| 20% | 31% |
| 50% | 53% |
| 80% | 64% |
As power increases, so does our confidence that a positive result is a real one.
Why This Matters for You
Statistical power isn’t just an academic concept; it’s a fundamental part of designing credible research.
- Before you start: Conducting a power analysis helps you determine the right sample size needed to detect your expected effect.
- Avoid wasted resources: Low-powered studies waste time, money, and effort, all while producing unreliable results.
- Build trust: High-powered studies produce robust, replicable findings that build confidence in your work.
In the end, a study without enough power is like trying to find a needle in a haystack with your eyes closed. By understanding and planning for power, you can open your eyes and give your research the best possible chance of success.